RainSim is an implementation of the spatial-temporal Generalized Neyman Scott Rectangular Pulses (NSRP) rainfall model. A brief overview is provided here, more details can be found in Burton et al, (2008) and Cowpertwait et al, (2002).

Neyman-Scott Rectangular Pulses Model

Figure 1 illustrates the model structure. Conceptually, storm events are simulated through time, each of which is associated with a number of raincells of given duration and intensity.

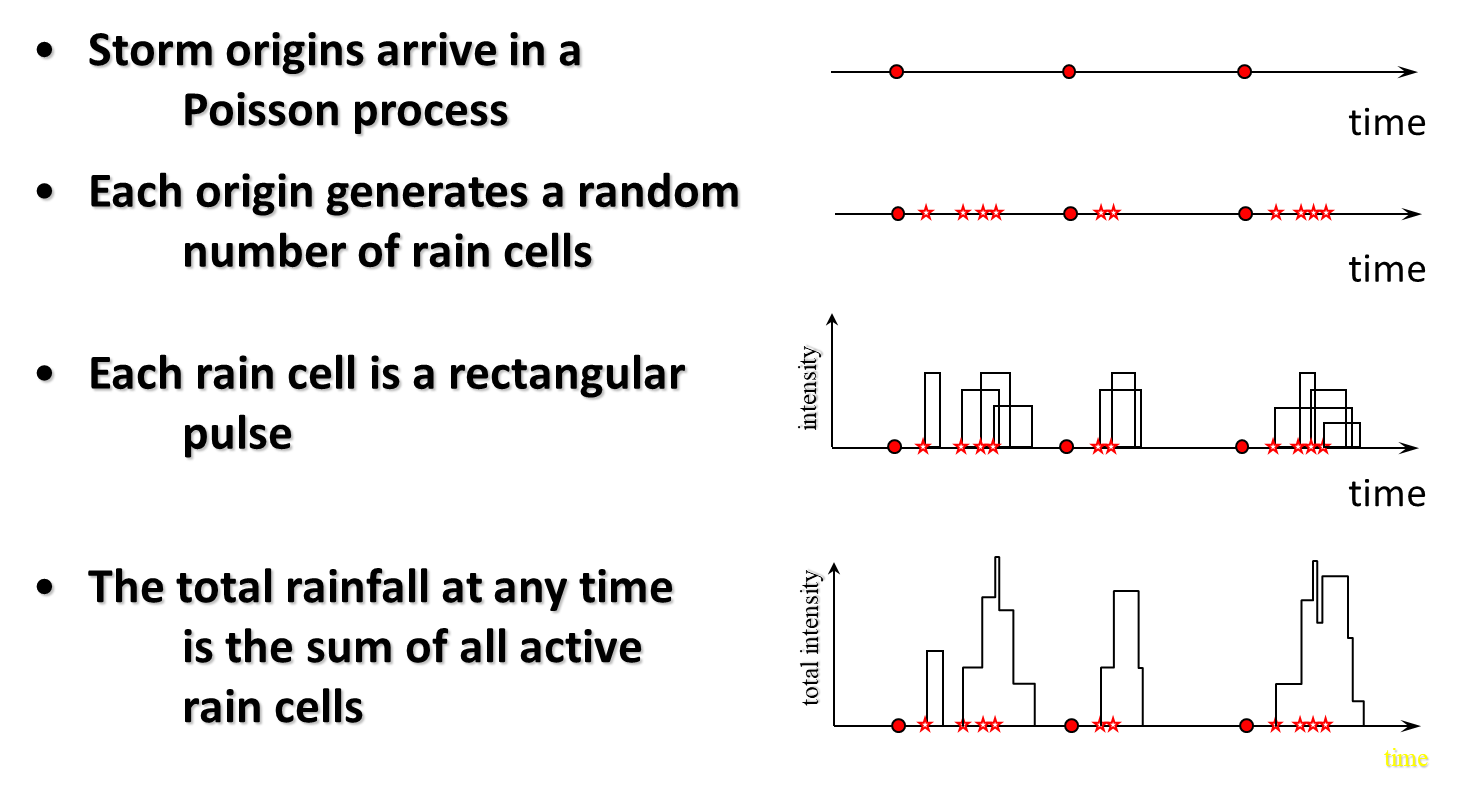Figure 1. Neyman-Scott Rectangular Pulses rainfall model

Spatial-Temporal and Generalized NSRP model

In the spatial-temporal RAINSIM model, rain cells occur randomly in space as discs, Figure 2. Over the duration of a cell’s lifetime, the rainfall intensity is uniform in both space and in time.

The Generalized model allows for the possibility of rain cells that can be conceptually considered as either stratiform (large area, low intensity) or convective (small area, high intensity)

The spatial-temporal and Generalized versions of the NSRP model are combined in RainSim.

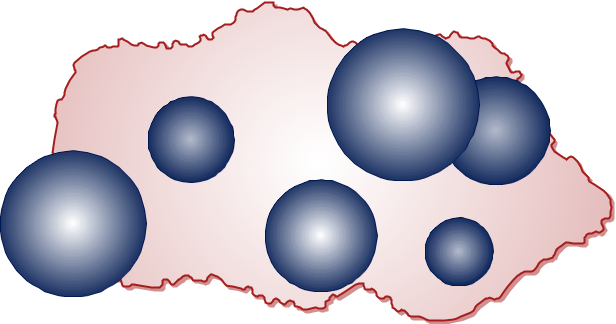
Figure 2. Neyman-Scott Rectangular Pulses space-time model.

The model is typically applied at the daily or hourly scale. However, hourly series can be dissaggregated using the empirical model of Ormsbee (1989).

Applying RainSim

A schematic of the procedure for applying RainSim is provided in Figure 3,

• Analysis involves calculating the statistics of interest from the observational time-series
• Fitting identifies the parameter set that most closely matches the observed statistics
• Simulation generates the synthetic time series, using the parameters from fitting
• Analysis involves evaluating the synthetic series against the observed statistics

The model can be fitted using a combination of statistics including the station mean, variance, dry-dry transition probability, and also the cross-correlation between stations. Monthly, daily and hourly statistics can all be included to capture the seasonal changes in rainfall characteristics. The chosen statistics should reflect the application, for example, the monthly variance may be of interest for groundwater applications, while hourly statistics are of interest for flooding.

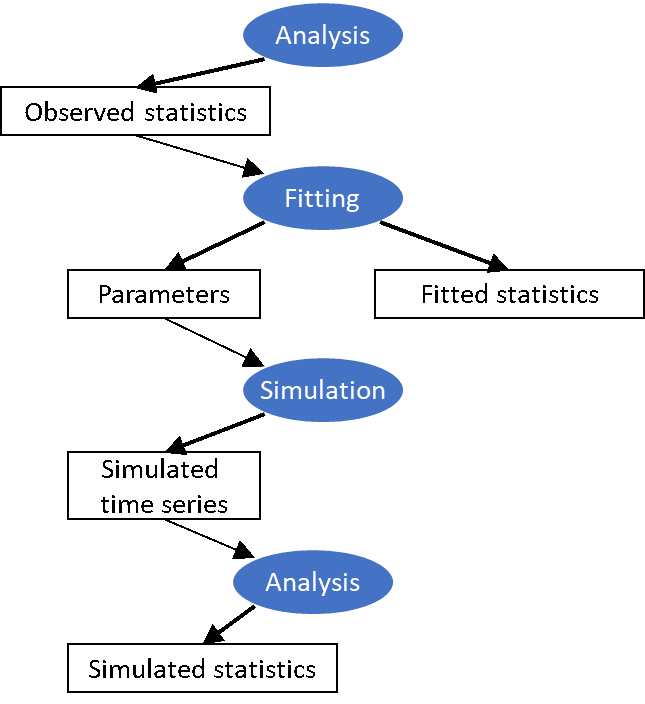
Figure 3. Schematic of applying RainSim

References

Burton, A., Kilsby, C.G., Fowler, H.J., Cowpertwait, P.S.P. and O'connell, P.E., 2008. RainSim: A spatial–temporal stochastic rainfall modelling system. Environmental Modelling & Software, 23(12), pp.1356-1369.

Cowpertwait, P.S.P., Kilsby, C.G., and O’Connell, P.E., 2002, A Spatial-Temporal Neyman-Scott Model of Rainfall: Empirical Analysis of Multisite Data, Water Resour. Res, 38, 8, 10.1029/2001WR000709

Fowler, H.J., Kilsby, C.G., and O’Connell, P.E., 2000 A stochastic rainfall model for the assessment of regional water resource systems under changed climatic conditions Hydrol. Earth Sys. Sci., 4, 261-280.

Ormsbee, L.E., 1989. Rainfall disaggregation model for continuous hydrologic modeling. Journal of Hydraulic Engineering, 115(4), pp.507-525.